Tutorial: Recursion and Algorithmic Art Using Processing
By Jim Plaxco

Illustration 1: Computer Art Created Using Recursion
Have you ever wondered how algorithmic artists go about creating art via computer programs? Algorithmic artists actually have a very large number of algorithms, mathematical formulas, and programming techniques available to them to create programs that create art. One programming concept used by algorithmic artists is recursion. This tutorial on recursion is intended for both novice programmers and collectors of algorithmic art who would like to have a better understanding of one of the many programming methods used by algorithmic artists.
What is a Function?
Before defining recursion, let's start by defining the term function. A function is a cohesive block of code or program statements that perform some specific task or tasks. A function may or may not require input data (aka variables) and it may or may not create output values. A function may also be referred to as a method, a procedure, a routine, or a subroutine.
One of the benefits of functions is that they allow a programmer to break down a large programming problem into smaller, more manageable components. Typically one function calls another function to perform some specialized task on some data or variables. As a part of this process, the called function may itself call one or more other functions to assist it in performing the task.
For example, in some function there may appear the following lines of code:
float mynumber = 4; float result = squareIt(mynumber);
The first line of the above code creates a numeric floating point variable with the name mynumber and assigns it a value of 4. The second statement calls the function squareIt and passes it the value contained in the variable mynumber. The squareIt function will compute the square of mynumber and place the result of that operation into the numeric floating point variable result. In this case the value will be 16.
Following is the source code for the function squareIt.
float squareIt(float value) {
return (value*value);
}
As you can see, the squareIt function does not call any other functions. It is frequently the case that in order to perform some more complicated task you'll have a situation where function A calls function B which calls function C and so on.
Now for Recursion
With recursion, we have the situation where a function calls itself one or more times. So a recursive function is a function which contains one or more calls to itself. A useful visual metaphor for recursion is that of the Matryoshka - the Russian nesting dolls where one doll holds another, smaller version of itself inside and that smaller doll has a smaller version of itself inside, and so on.
With recursive functions it's critical to have a terminating condition - also referred to as a base case. This is a condition or rule that will cause the function to stop calling itself. Without such a terminating condition, the function would call itself forever - or until it consumed all the system resources available to it.
The principal benefit to programmers of using recursion is that the programmer has less code to write and maintain. However, designing a recursive function does require additional thought and planning.
Algorithmic Art and Recursion
For the algorithmic artist, the beauty of recursion is that it provides a way to create complex visual forms from a simple beginning using simple rules. To illustrate the concept of recursion, I've written a short program for the Processing platform1. The program contains the recursive function Recursion_Art(). As you can see in the source code below, the recursive function Recursion_Art() is quite simple. It consists of
- a command to draw a rectangle - rect()
- an if statement to test for the terminating condition (base case)
- four calls to itself.
I have used the picture created by this program to illustrate this article (see Illustration 1). What makes this visual complexity possible is the transformation that is applied to the rectangle when the Recursion_Art() function is called. Each time Recursion_Art is called, it calls itself an additional four times passing to the next iteration of the function the x,y coordinates of each corner of the rectangle it has just drawn, and a new, smaller size for the next set of rectangles.
Recursion_Art() is initially called inside the draw() function, which is a Processing function that executes continuously. The Recursion_Art() function expects to receive four values, an x and y which defines the location of the center of the rectangle to be drawn, and a width and a height which defines the size of the rectangle to be drawn.
// Processing Source Code for Recursion_Art.pde
// By Jim Plaxco, www.artsnova.com
static final int LIMIT=6; // size of the smallest rectangle to draw
// System Setup Function
void setup() {
size(600,400); // canvas/screen size
background(255); // canvas/screen background color, 255=white
stroke(0); // draw color, 0=black
fill(126); // fill color, 126= mid-gray
rectMode(CENTER); // use x,y as rectangle center
}
// System Draw Function
void draw() {
if(frameCount==1) Recursion_Art(width/2,height/2, width/2,height/2);
}
// Recursion_Art Function
// Input Parameters: x,y = center of rectangle
// w,h = width and height
// Return Value: None (void)
void Recursion_Art(int x, int y, int w, int h) {
rect(x,y,w,h);
if(w > LIMIT)
{ // the size of the current rectangle is larger than the LIMIT value
Recursion_Art(x-(w/2), y-(h/2), w/2, h/2);
Recursion_Art(x+(w/2), y-(h/2), w/2, h/2);
Recursion_Art(x-(w/2), y+(h/2), w/2, h/2);
Recursion_Art(x+(w/2), y+(h/2), w/2, h/2);
}
}
In the example given, the function Recursion_Art executed 5,461 times - meaning that 5,461 rectangles were drawn on the screen. The depth of recursion is 7. Think of depth as equivalent to generations of offspring.
- The draw() function, calls Recursion_Art()
- which then calls Recursion_Art() four times
- each of which call Recursion_Art() four times
- each of which call Recursion_Art() four times
- each of which call Recursion_Art() four times
- each of which call Recursion_Art() four times
- each of which call Recursion_Art() four times
It is at the final level that the width of the current rectangle being drawn finally drops below the limit that has been set, thus causing the process to come to a stop.
Recursion is most powerful graphically in its ability to create complex, repeating patterns. In fact the nature of the patterns can be changed by making small, simple changes to the program. For example, commenting out the rectMode() function in the program results in the image seen in Illustration 2.

Illustration 2: Alternate version of Recursion Art
Deterministic vs Non-deterministic Functions
The recursive function I have presented here is called deterministic. With a deterministic algorithm, given the same inputs, the output will always be the same. In other words, no matter how many times you run the Recursion_Art.pde program, the output will always be identical.
Alternatively, a non-deterministic function can be used to produce different results every time by incorporating random factors into the algorithm. I have rewritten the four recursive call statements in the Recursion_Art function below so that they incorporate the random number function. Now the numbers being passed to the Recursion_Art function are no longer consistent from one run to the next.
// Recursion_Art Function
// Input Parameters: x,y = center of rectangle
// w,h = width and height
// Return Value: None (void)
void Recursion_Art(int x, int y, int w, int h) {
rect(x,y,w,h);
if(w > LIMIT)
{ // the size of the current rectangle is larger than the LIMIT value
Recursion_Art(x-((w/2)+int(random(-w*.4, w*.4))),
y-((h/2)+int(random(-h*.2, h*.2))),
(w/2)+int(random(-w*.4, w*.4)),
(h/2)+int(random(-h*.2, h*.2)));
Recursion_Art(x+((w/2)+int(random(-w*.4, w*.4))),
y-((h/2)+int(random(-h*.2, h*.4))),
(w/2)+int(random(-w*.4, w*.4)),
(h/2)+int(random(-h*.2, h*.2)));
Recursion_Art(x-((w/2)+int(random(-w*.4, w*.4))),
y+((h/2)+int(random(-h*.2, h*.2))),
(w/2)+int(random(-w*.4, w*.4)),
(h/2)+int(random(-h*.2, h*.2)));
Recursion_Art(x+((w/2)+int(random(-w*.4, w*.4))),
y+((h/2)+int(random(-h*.2, h*.4))),
(w/2)+int(random(-w*.4, w*.4)),
(h/2)+int(random(-h*.2, h*.2)));
}
}

Illustration 3: Output from the Non-deterministic version of Recursion Art
Recursion and Color
In addition to modifying the drawing statements, simple rules for generating color can be added to the function. In Illustration 4 below, the patterns of color were generated by mapping the remainder of the squares of the coordinates onto a color range.
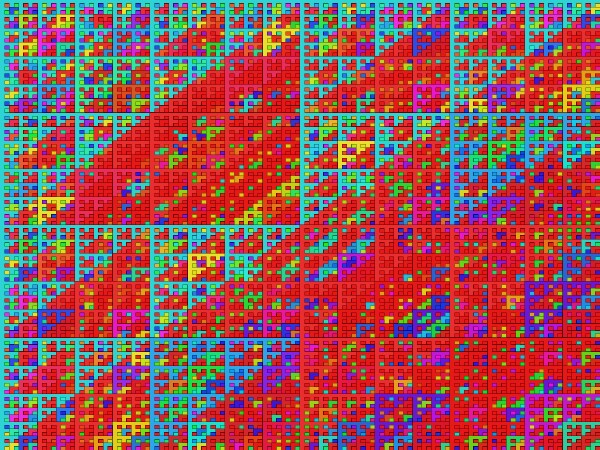
Illustration 4: Color Recursion Art
Recursion is a very powerful technique and actions as simple as altering the call sequence; relocating the drawing command; changing the basic drawing shape (like replacing the rectangle with an ellipse); or altering scaling factors can result in the creation of radically different images.
Recursive Recursion
The examples of recursion that I've provided demonstrate what can be accomplished using a single simple recursive function. Imagine what more can be done when one recursive function calls another different recursive function which calls yet another different recursive function.
Footnotes
1. If you want to experiment with the program Recursion_Art.pde, you will need to download and install Processing. Processing is free and is available for multiple platforms. Visit http://processing.org/ for more information and to download Processing for your computer.
“To iterate is human, to recurse divine.”
L. Peter Deutsch